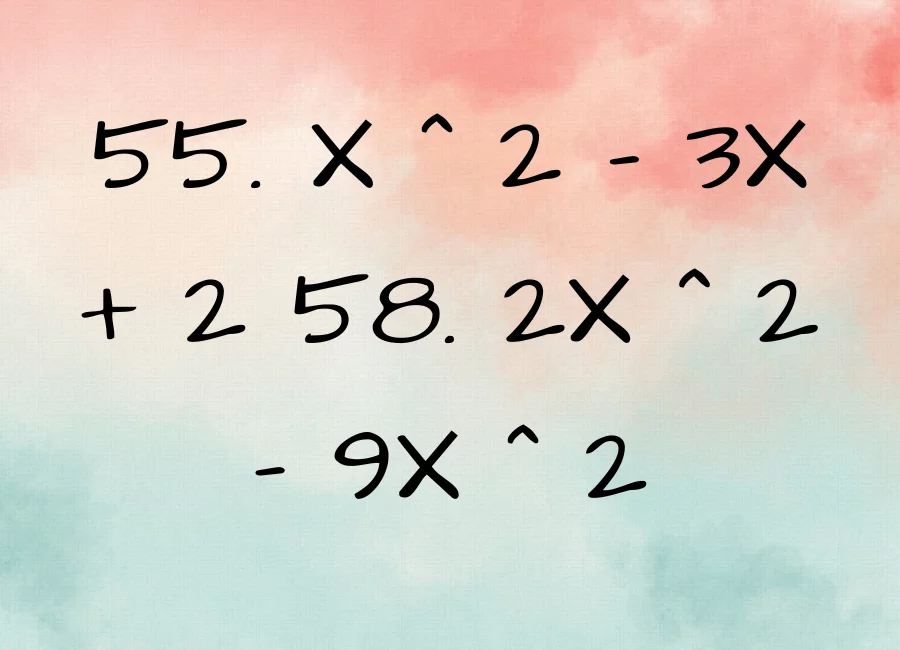55. x ^ 2 – 3x + 2 58. 2x ^ 2 – 9x ^ 2. Quadratic equations are an essential part of algebra and mathematics. They are second-degree polynomial equations and find applications in various fields, including physics, engineering, and computer science. In this article, we will explore the fundamentals of quadratic equations, and different methods of solving them, and then analyze two specific equations: 55. x^2 – 3x + 2 and 58. 2x^2 – 9x^2.
Understanding Quadratic Equations 55. x ^ 2 – 3x + 2 58. 2x ^ 2 – 9x ^ 2
What are Quadratic Equations?
A quadratic equation is a second-degree polynomial equation of form ax^2 + bx + c = 0, where ‘x’ represents an unknown variable, and ‘a,’ ‘b,’ and ‘c’ are constants, with ‘a’ not equal to zero. The highest power of the variable ‘x’ is 2, making it a quadratic equation.
Standard Form of a Quadratic Equation
The standard form of a quadratic equation is given by ax^2 + bx + c = 0. It provides a clear representation of the coefficients ‘a,’ ‘b,’ and ‘c.’
Discriminant and Nature of Roots
The discriminant, denoted by Δ, plays a crucial role in determining the nature of the roots of a quadratic equation. It is calculated as Δ = b^2 – 4ac. The nature of the roots is determined as follows:
- If Δ > 0, the quadratic equation has two distinct real roots.
- If Δ = 0, the quadratic equation has two identical real roots.
- If Δ < 0, the quadratic equation has two complex roots.
Solving Quadratic Equations
There are various methods to solve quadratic equations, and we will discuss three common approaches.
Factoring
Factoring involves breaking down the quadratic equation into two binomial equations and solving for ‘x.’ This method is effective when the equation can be easily factored.
Quadratic Formula
The quadratic formula is a universal method for solving any quadratic equation. It is given by x = (-b ± √Δ) / 2a. This formula works for all quadratic equations, regardless of whether they have real or complex roots.
Completing the Square
Completing the square is an algebraic technique that allows us to rewrite a quadratic equation in the form (x – h)^2 = k. By applying this method, we can find the values of ‘x.’
Analysis of the Given Equations
Equation 1: 55. x^2 – 3x + 2
Let’s analyze the given equation: 55. x^2 – 3x + 2.
Discriminant Calculation
For this equation, a = 1, b = -3, and c = 2.
Δ = (-3)^2 – 4 * 1 * 2 = 9 – 8 = 1
The discriminant (Δ) is positive (Δ > 0), which means the equation has two distinct real roots.
Finding the Roots
Using the quadratic formula, we can find the roots of the equation:
x = [3 ± √1] / 2 * 1 x = [3 ± 1] / 2
So, the roots of the equation 55. x^2 – 3x + 2 are: x₁ = (3 + 1) / 2 = 4 / 2 = 2 x₂ = (3 – 1) / 2 = 2 / 2 = 1
Therefore, the roots are x = 2 and x = 1.
Equation 2: 58. 2x^2 – 9x^2
Now, let’s analyze the given equation: 58. 2x^2 – 9x^2.
Discriminant Calculation
For this equation, a = 2, b = 0 (since -9x = 0x), and c = 0.
Δ = 0^2 – 4 * 2 * 0 = 0 – 0 = 0
The discriminant (Δ) is zero (Δ = 0), which means the equation has two identical real roots.
Finding the Roots
Using the quadratic formula, we can find the roots of the equation:
x = [0 ± √0] / 2 * 2 x = 0 / 4
So, the root of the equation 58. 2x^2 – 9x^2 is: x = 0
Also Read:
Conclusion
In conclusion, quadratic equations are essential mathematical tools used to solve problems in various fields. They have real or complex roots depending on the discriminant value. In our analysis of the given equations 55. x^2 – 3x + 2 and 58. 2x^2 – 9x^2, we found that the first equation has two distinct real roots, while the second equation has two identical real roots.
Remember, understanding quadratic equations is fundamental for further studies in mathematics and its applications in the real world.